Por Román Ceano

Tiltman era un experto criptoanalista que había estudiado además la monografía sobre el cifrado Vernam escrita por el director de investigación de su departamento, Gerry Morgan. Eso le hizo reaccionar eléctricamente al enterarse del hallazgo. Él en persona se puso a trabajar sobre la transcripción.

Siguiendo las ideas de Morgan, aplicó una curiosa propiedad del cifrado Vernam. Tomó los dos textos cifrados y los sumó (en el sentido explicado más arriba). Con ello obtuvo una ristra de caracteres que era la suma de los dos textos en claro. En efecto; si P1 y P2 son los textos en claro a los que sumamos la secuencia K para obtener los textos cifrados C1 y C2, al sumar C1+C2 obtenemos P1+P2, puesto que C1+C2=(P1+K)+(P2+K) y K+K=0 (entendiendo por 0 el elemento neutro de esta aritmética). Nótese que si se suman dos textos iguales cifrados con la misma clave, el resultado es una secuencia de elementos neutros, por lo que los pequeños cambios que introdujo el operador fueron lo que permitió el ataque.

Tiltman trabajaba con la tabla de sumas, en la que aparecían caracteres calculados al operar sus representaciones en cinco bits. Una vez hubo eliminado la secuencia de cifrado y sabiendo que cada carácter del texto resultante era la suma de dos que en el mensaje original distaban unas pocas posiciones, lo descifró en diez días, algo que desde entonces ha desconcertado a sus admiradores, porque no parece que sea tan difícil para alguien como él.

Seis meses después, cuando abandonó los mensajes japoneses y decidió volcarse en el teletipo alemán tras recibir la nota de Kenworthy, encontró en el dossier el texto en claro descifrado por él junto con la copia de una nota en la que informaba a Travis que ese resultado era irrelevante porque no era probable que nunca más se obtuviera una pareja de mensajes como aquella. Mas aún, la complejidad de la secuencia cifradora era tal, que sin conocer la naturaleza del aparato que la generaba no había ninguna esperanza de poder descifrar el Geheimschreiber. Probablemente sonrió al ver su propia nota porque mientras él se rompía la cabeza contra los cifradores silábicos japoneses, uno de los subordinados de Morgan había descrito las reglas generatrices de la secuencia.

Nigel de Grey, uno de los participantes en el descifrado del telegrama Zimmerman y por tanto una leyenda viviente en BP, no se cansó nunca de decir que Bill Tutte había obtenido uno de los grandes éxitos de toda la guerra al desentrañar la estructura de esa secuencia.

Un subproducto del descifrado del mensaje doble realizado por Tiltman, era que sumando el texto en claro a cualquiera de los dos mensajes cifrados interceptados se obtenía la ristra de caracteres que se había sumado para cifrarlos. Los pesos pesados del departamento la tomaron en sus manos con la esperanza de hallarle una lógica bajo la apariencia aleatoria.

Si los alemanes habían inventado una fuente de secuencias aleatorias que se pudieran sincronizar no había esperanza, pero quizás se trataba meramente de un sistema de ruedas con los ciclos ocultos, bien por una longitud enorme o por alguna ocurrencia desconocida. Nadie había visto una de esas máquinas y los vagos comentarios de Wohlrab eran la única referencia de tamaño que se tenía. De ellos se deducía que en caso de ser ruedas, éstas no podían ser muy grandes. Se les calculaba un máximo de 50 posiciones a cada una y un máximo de tres ruedas por posición (es decir 15 ruedas en total).

Tutte era un estudiante de química de Cambridge que hasta ese momento había tenido un estatus más bien bajo en el departamento de investigación. En navidad, cuando todo el mundo estaba harto de darle vueltas sin resultado, Morgan se acercó a su mesa y le dijo “Mira qué puedes hacer con esto...”.

Tutte no creía que pudiera hacer gran cosa, pero por no parecer negativo se puso a aplicar un método que les habían enseñado en el cursillo de reclutamiento. Se trataba del método Kasiski, que consiste en buscar repeticiones y luego escribir el mensaje formando líneas iguales a la distancia entre estas. Al poner las líneas una encima de otra, podían aparecer patrones repetitivos más cortos que permitieran repetir la operación. Aunque el Kasiski fue diseñado para romper el cifrado Vigenere, resultaba útil en general para descubrir cualquier periodicidad en la clave en una gran variedad de cifrados.

Tutte tomó el primer bit de cada uno de los cuatro mil caracteres y lo escribió pacientemente en líneas de 575, ya que varios compañeros sospechaban que la secuencia de primeros bits tenía su origen en tres ruedas, una de 23 posiciones, otra de 25 y una tercera de tamaño desconocido. Tutte encontró algunas repeticiones de series de cruces y puntos pero notó que se desplazaban hacia la izquierda una posición por línea.

Esto le llevó a copiar la secuencia otra vez pero en segmentos de 574. Esta vez sí que obtuvo largas series iguales en las mismas posiciones, pero separadas por muchas líneas. A continuación probó 41, que es un divisor primo de 574, y que podía por tanto ser el tamaño de una de las tres ruedas supuestas. Copiando en líneas de 41, aparecieron una cantidad de repeticiones que mostraban que sin duda existía una fuente periódica con esa longitud.

Satisfecho con esa certeza, se puso a trabajar en la longitud de las otras dos ruedas. A pesar de que examinó toda la secuencia utilizando el patrón 41, no logró cuadrar ninguna pareja de longitudes compatible con los datos. Cuánto más claro estaba que el 41 creaba un paisaje de similitudes, más oscuro resultaba discernir el porqué de las diferencias. Éstas parecían tener una lógica pero no encajaba en ninguna serie cíclica, como si fueran ciclos que cambiaran de longitud.

Tutte se dio cuenta de que lo que separaba esos ciclos de tener una longitud fija estaba relacionado con la extraña tendencia estadística que mostraba la serie a la repetición, de forma que una cruz tenía una probabilidad alta de ser seguida por otra cruz, y lo mismo para los puntos. Esta tendencia no provenía ciertamente de la fuente cíclica ya descrita, sino de algún tipo de fuente aperiódica que se sumaba. No podía tener su origen en una combinación de dos ruedas adicionales, sino que parecía provenir de una sola, aunque bien extraña.

En sus memorias, Tutte describe la solución al misterio de la rueda que cambiaba de tamaño mientras causaba un sesgo hacia la repetición de puntos o cruces en la secuencia, como la conclusión inevitable del razonamiento que había desarrollado. Mientras que la rueda de 41 se movía siempre un paso, había una segunda rueda de 43 posiciones que se quedaba quieta o avanzaba siguiendo algún tipo de patrón todavía desconocido.

Tanto si esa solución se le apareció en un súbito relámpago como era proverbial en los matemáticos, o si emergió de su niebla mental mientras garabateaba frenéticamente como les solía suceder a los lingüistas de la generación de De Grey y Knox, sabemos que no era evidente para sus contemporáneos, porque el hallazgo le valió a Tutte una gran dosis de la gloria secreta característica de BP.

Curiosamente, en su caso hubo un premio adicional. Además de las palmadas y aplausos en la intimidad de su cobertizo, y de las ocasionales miradas de admiración en el jardín o en el comedor de parte de los pocos que estaban en el secreto, Tiltman consiguió que la universidad de Cambridge le diera el doctorado sin necesidad de acabar la carrera ni presentar la tesis, alegando que “su trabajo para el gobierno demuestra suficientemente su valía intelectual”.

La vía abierta por Tutte conducía al corazón del cifrado de la Geheimschreiber. Lo que había descrito para la secuencia del primer “bit” fue aplicado por sus compañeros a las otras cuatro. Era en efecto posible describir esas secuencias asumiendo también sólo dos ruedas para cada una. La primera debía girar siempre una posición para cada carácter, mientras la segunda lo hacía siguiendo un patrón de desconocido. En medio de un gran entusiasmo, la sección fue estableciendo los tamaños de las ruedas de cada pareja.

El golpe final a la estructura interna del generador de secuencias fue establecer que los avances o no-avances de las segundas ruedas se daban al unísono para las cinco secuencias y siguiendo un patrón aperiódico. Conocidos los tamaños de las ruedas que formaban las cinco parejas y en posesión del secreto de cómo generar secuencias aperiódicas, se culminó alegremente la descripción, postulando la existencia de dos ruedas más, una de las cuales giraba siempre y gobernaba el giro de la segunda, que sólo se movía en las cruces de la primera (ver esquema).

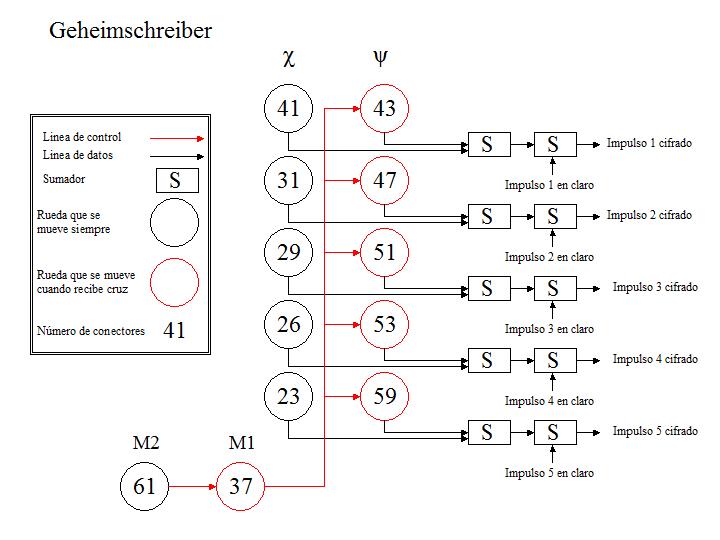
Las ruedas inferidas eran muy diferentes de las de Enigma. Las ruedas de Enigma eran la expresión eléctrica de una permutación practicada sobre el alfabeto. Haciendo abstracción del reflector y el panel de conexionado, la máquina Enigma cifraba cada carácter con un alfabeto diferente a base de variar la forma en que sumaba los tres fijos que contenían sus ruedas.

En cambio, se suponía que las ruedas de la Geheimschreiber consistían en un número dado –diferente para cada rueda- de conectores que dejaban pasar o no la electricidad según la manipulación que hubiera hecho el operador durante la configuración. Si todos estaban conectados, la rueda suministraba una secuencia de cruces. Si por ejemplo, todos menos uno estaban conectados en una rueda de 41 conectores, suministraría 40 cruces y un punto. Colocando dos ruedas y un circuito de adición booleana, se obtiene un superciclo con una longitud múltiplo del número de conectores de ambas.

En el Geheimschreiber cada posición (cada “bit”) de la letra creada tenía origen en un par de ruedas. La primera giraba siempre una posición para cada carácter mientras la segunda sólo giraba a veces, como dedujo Tutte. Las cinco ruedas que giraban siempre fueron denominadas en BP como ruedas Chi, mientras las que giraban sólo a veces, se denominaron ruedas Psi.

Las otras dos ruedas eran las que gobernaban el giro de las ruedas Psi. Aunque al principio se denominaron también con una letra griega, luego esta denominación se perdió y pasaron a ser nombradas como “ruedas motoras”. Cuando la rueda motora 1 dejaba pasar la corriente (“mostraba una cruz”) todas las ruedas Psi se movían una posición. El movimiento de esta rueda motora 1 estaba a su vez gobernado por la rueda motora 2 siguiendo el mismo criterio. La rueda motora 2, al igual que las ruedas Chi, se movía siempre una posición.

La secuencia de caracteres estaba condicionada a qué conectores estuvieran activados en cada rueda, es decir cuales dieran cruces y cuales puntos, así como a cual fuera la posición inicial de las ruedas. Cada juego de posiciones de los conectores determinaba un superciclo, de forma análoga a como en la Enigma cada juego de posiciones de las ruedas en sus huecos determinaba una sucesión de alfabetos diferentes. Esta configuración de conectores se cambiaba con una cierta periodicidad, pero lo que hacía que cada mensaje fuera diferente era la posición de las ruedas al empezar el mensaje.

Esta posición se comunicaba del emisor al receptor mediante un sistema de indicadores. El sistema de indicadores de la Geheimschreiber consistía en doce letras nombradas en claro mediante palabras mnemotécnicas (Anton para ‘a’, Berta para ‘b’, Cesar para ‘c’, etc...). Cada letra representaba la posición de una de las doce ruedas. Los operadores disponían de una tabla para consultar, ya que no era un sistema consecutivo sino totalmente arbitrario para dificultar la intercepción. Los interceptores no sabían qué posición representaba cada letra, pero sí que podían identificar mensajes cifrados con claves muy parecidas o iguales.

Aparte de facilitar la identificación de mensajes cifrados con la misma clave a los criptoanalistas enemigos, otro problema evidente del método de indicadores que usaban los alemanes era que al tener la mayor parte de ruedas –todas menos las motoras- más posiciones que las letras disponibles, algunas posiciones no se usaban nunca. Por ello, las posibles posiciones iniciales eran 26^12 por cada configuración de conectores.

Resulta tentador multiplicar ese resultado por el número de dichas configuraciones, pero esto resulta engañoso. Era necesario un equilibrio de cruces y puntos en cada rueda para que el sistema no resultara trivial, por lo que no todas las configuraciones eran posibles ni mucho menos. Tutte en sus memorias dice que su éxito fue producto de una distribución deficiente de las cruces y puntos, y que con las configuraciones más evolucionadas utilizadas a partir del verano de 1942 nunca hubiera podido desentrañar la secuencia. Esto ilustra la sutilidad del método y su dependencia de un uso inteligente. Un configurador hábil puede lograr que la secuencia cifradora tenga unas proporciones de cada carácter tales que el criptotexto sea aleatorio a todos los efectos.

Pero incluso suponiendo por mor del argumento una proporción muy pequeña de configuraciones utilizables, Geheimschreiber ofrecía claramente un cifrado mucho más fuerte que Enigma. Cuando Tiltman decidió lanzar sobre él todo el peso de sus equipos de choque, no estaba nada claro que pudieran triunfar.

El único indicio optimista era una especie de leyenda que había llegado por varios conductos diferentes. Algunas fuentes indirectas afirmaban que los suecos habían descifrado mensajes de una variante de la Geheimschreiber. Al parecer habían pinchado el cable que pasaba por su territorio en dirección a la ocupada Noruega y habían logrado leer una cantidad indeterminada de mensajes.

(C) Román Ceano. Todos los derechos reservados.