Por Román Ceano

Decir que las permutaciones tienen estructura de grupo significa que: a) si operamos dos de ellas, obtenemos también una permutación, b) existe una permutación que al aplicarla a las demás las deja igual, c) para cada permutación existe otra llamada inversa y al operar ambas se obtiene la descrita en ‘b’, y d) si operamos dos y el resultado lo operamos con una tercera es lo mismo que si operamos la tercera con la segunda y luego operamos con la primera. La mayoría de objetos matemáticos poseen estas propiedades junto a muchas otras, pero las permutaciones no poseen apenas ninguna más. Estas propiedades descritas para las permutaciones permiten operar ecuaciones y despejar variables pero de una forma rudimentaria puesto que no se puede cambiar el orden, ni redistribuir, ni sacar factor común. A Rejewski no le preocupaba esto porque, aunque laborioso, es trivial operar con ellas. Lo que le preocupaba era la escasez de variables conocidas en sus ecuaciones. Para poder resolver un sistema hacen falta tantas ecuaciones como incógnitas y éste distaba de ser el caso.

Si hubieran sido ecuaciones de números reales, no habría hecho falta seguir para saber que existían infinitas soluciones y por tanto ninguna. Pero además de las propiedades que las caracterizan como grupo, se conocían un par más exclusivas de las permutaciones que podían permitir restringir el conjunto de soluciones. Para describir una de estas propiedades, debemos entrar brevemente en la tipología de las permutaciones descrita primeramente por Rufini.

Una permutación se divide en sustituciones y una permutación que caracterice un alfabeto de 26 letras tiene 26 sustituciones (la J se convierte en V, la X se convierte en L, etc...). En algunas permutaciones -como por ejemplo en la permutación identidad (a,b,c,d,...), que es el elemento neutro al que se aludía más arriba- nunca pasa que la letra final de ninguna sustitución sea la letra origen de otra. Sin embargo hay muchas otras permutaciones en las que sí sucede. Por ejemplo, si tomamos el alfabeto (b,c,d,e,...) que hace corresponder a cada letra la siguiente, el destino de la primera sustitución es el origen de la segunda, el de la segunda la tercera, etc..., por lo que la permutación forma un “ciclo”. Además de las permutaciones con 26 ciclos y las permutaciones con un solo ciclo existen todas las posibilidades intermedias. Puede ser que una permutación tenga tres ciclos de cuatro sustituciones, uno de ocho y otro de seis o cualquier combinación de ciclos que al final sume las 26 sustituciones. Además de denotar una permutación mediante su alfabeto también podemos hacerlo describiendo sus ciclos. Esta notación es muy utilizada, porque es más compacta y visualiza la estructura interna de la permutación.

Existe una propiedad asociada con la estructura de ciclos cuyo enunciado dice que si tenemos dos permutaciones que tengan la misma estructura de ciclos, existirá una tercera tal que al operar la segunda con ella y con su inversa obtendremos la primera. Se dice que las dos primeras son conjugadas una de la otra y por tanto se puede enunciar la propiedad diciendo que dos permutaciones tienen la misma estructura de ciclos si y solo si son conjugadas. La utilidad de esta propiedad es que permite descomponer cualquier permutación en dos, y una puede ser escogida arbitrariamente porque nos conviene para el manejo de las ecuaciones. Sin embargo tiene la limitación de que ello sólo es posible si tienen la misma estructura de ciclos, por lo que antes de utilizar la propiedad hay que demostrar (o suponer) que la tienen y ser consciente de que la compartirán con la tercera. También permite determinar la estructura de ciclos de permutaciones desconocidas si conocemos la estructura de ciclos de una conjugada y, en general ,es una gran ayuda para operar.

Rejewski determinó rápidamente que -por definición- las permutaciones A, B, C, D, E y F son conjugadas de la permutación R que representa el rotor ya que:

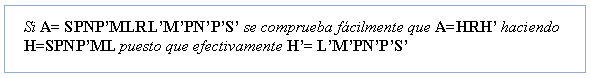
Como son conjugadas comparten el número de ciclos con R y por tanto tienen 13 ciclos de dos sustituciones (13 ciclos de longitud 2). Por ello son simétricas y al operarlas consigo mismas se obtiene el elemento neutro. Las permutaciones A, B, C, D, E y F varían cada día, pero Rejewski disponía de los alfabetos de las composiciones AD, BE y CF para casi todos los días.

Como prolongación de su estrategia de considerar que sólo la rueda rápida se movía durante la generación de esta colección de permutaciones, describió la permutación Q como la permutación inducida por toda la parte de Enigma que no se movía, es decir el reflector y las otras dos ruedas, obteniendo por tanto :

Este sistema sigue siendo irresoluble porque aún hay más incógnitas que ecuaciones, por lo que la vía parecía cerrada. Pero Rejewski no se detendría hasta agotar todas las posibilidades. Estudió cómo se relacionaban las permutaciones con sus composiciones a base de describir cuidadosamente todas las propiedades implicadas. Puesto que había demostrado que las composiciones A, B, C, D, E y F tenían sólo ciclos de longitud 2, dedicó toda su atención a composiciones de permutaciones que tuvieran esa característica. A base de horas encontró una nueva propiedad no citada en ninguna bibliografía anterior. Demostró, con el mismo rigor con el que lo habría hecho en una tesis doctoral, que la composición de permutaciones que sólo tengan ciclos de longitud 2 da lugar siempre a permutaciones con un número par de ciclos. Comprobó con gran satisfacción que todas las composiciones AD, BE y CF para todos los días en que tenía datos cumplían esta condición.

Esto representaba un avance, ya que es una restricción fuerte y por tanto su sistema de ecuaciones tenía menos grados de libertad de los que determinaba una mera comparación entre número de ecuaciones y número de incógnitas. Aún así calculó que había 7020 combinaciones de permutaciones que satisfacían tanto el sistema de ecuaciones como esta nueva restricción que había descubierto. Había reducido extraordinariamente las posibilidades ,pero aún no era posible dar el golpe final. A estas alturas Rejewski se daba cuenta de que estaba ante un premio mayor. La cima donde terminaba la vía que estaba abriendo era nada menos que el cableado de la rueda que ocupaba ese trimestre la posición rápida, y a partir de allí el de las otras dos. Pero si bien el ejército de espectros de matemáticos del pasado dirigidos por la mano maestra de Rejewski se había abierto camino hasta allí, ese mismo saber indicaba que era una vía muerta, porque aún quedaban demasiadas variables desconocidas.

 

© Román Ceano. Todos los derechos reservados.